Flare-On 12 Challenge 8 Writeup - FlareAuthenticator
Bag of Tricks: IDA, Python, Z3, CheatEngine, System Informer
Challenge 8
Recon
We receive an .exe file that is only 800 KB (nice!) and a bunch of DLLS (probably for compatibility sake) as long with a run.bat file stating:
1
2
3
@echo off
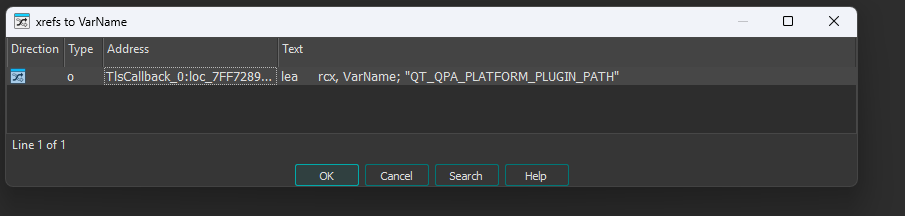
set QT_QPA_PLATFORM_PLUGIN_PATH=%~dp0
start %~dp0\FlareAuthenticator.exe
Just setting the environment variable to the current local path and executing, weird.. The executable is also a c++ written GUI using Qt6.
Verifying DLLs
To make sure the DLLs are legit I checked each one’s signature via Windows Explorer: 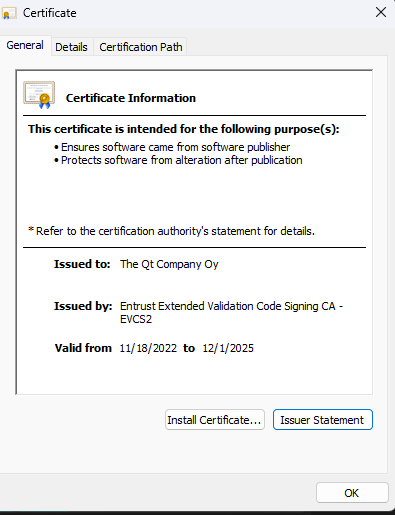
Bypassing run.bat
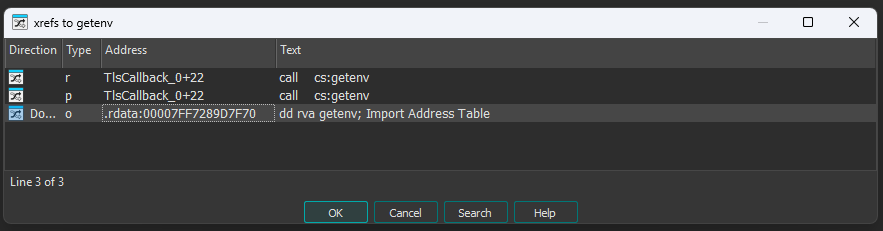
Opening the binary in IDA I first noticed there is a TLS Callback registered (will execute before main) that checks the environment variable the run.bat just set.
Because it is the only xref to said variable i’m gonna make a bold statement and just patch a return to the start of the function, so I can debug nicely (setting the environment variable can also work, but my VM got corrupted and I was researching this on my host).
Trying to Get a Callback on OK
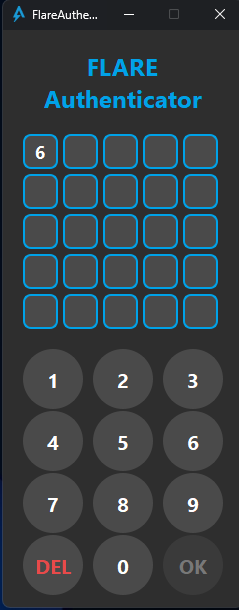
Running the program we get a nice calculator looking GUI
When pressing a button the DEL button lights up (probably because we can delete chars now) but the OK button (I guess submit) stays greyed out
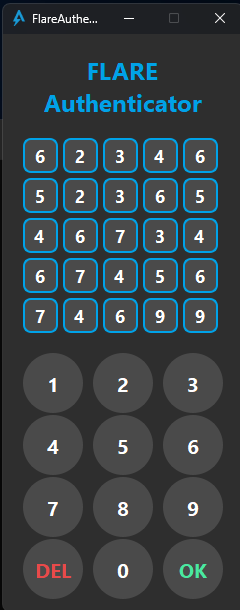
Only when filling up the entire 25 digit code we can press OK:
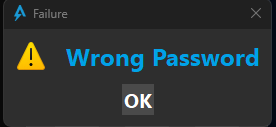
Granting us with a “Wrong Password” dialog
Obviously the challenge right now is get a callback on “OK”, the password checking logic probably happens over there. Having worked with this library before, this is a warning dialog box, so I’ll set a breakpoint on the the calling function to the module
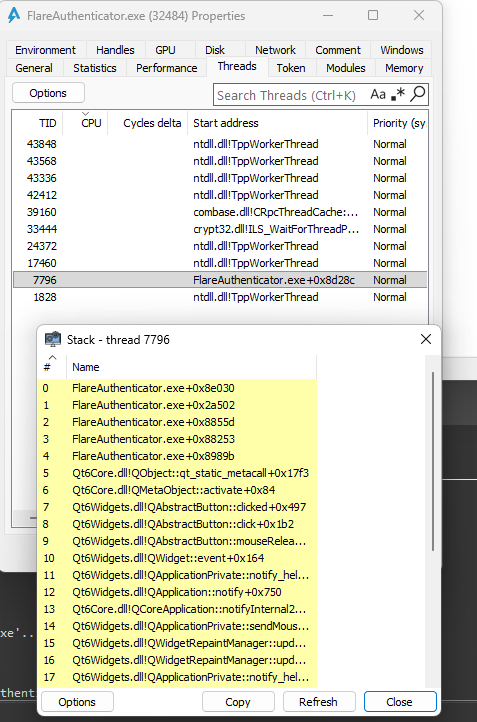
Now after hitting the breakpoint I’ll observe the callstack and go up until finding a beefy function that looks to do calculations/comparisons.
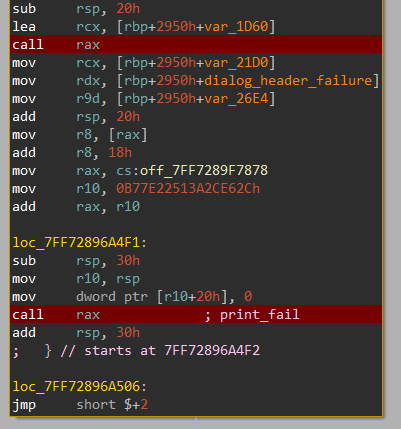
Going up just one call gets us to a huge, obfuscated function:
And as expected the params are loaded and print fail is called, let’s observe more of this function. Because this function is so large I spent a while just tracing the xrefs to the params and going up finding nothing. Then I thought, I just need to find the password hashing logic, than trace the hash/comparison using a hardware breakpoint all the way to this function ok_pressed.
Using CheatEngine to Locate “do_program”
I have one more ace up my sleeve, using CheatEngine like old times to find occurrences of the plaintext password in memory. To set this up I just start the FlareAuthenticator mysef, attach to it via CheatEngine and after locating the bytes detach CheatEngine and attach via debugger in IDA, then setting a hardware read/write breakpoint on the plaintext buffer.
Nice, now setting the breakpoint and continuing execution we actually hit something!
And it’s caller
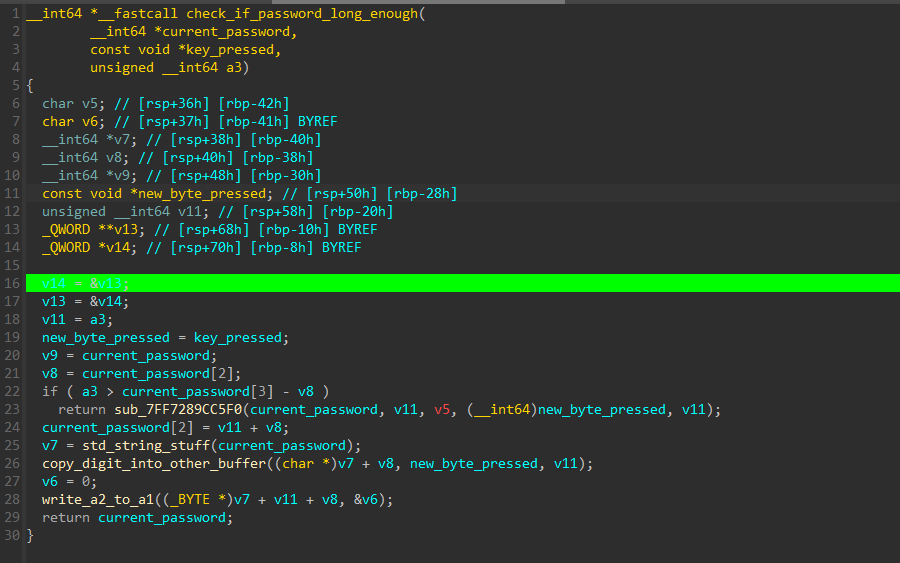
After setting more memory breakpoints I didn’t hit anything exciting, I was hoping to get an offset in ok_pressed (of the hashing or comparison) and spent quite a while doing this. Some time has passed and I though, maybe the secret/hash is generated digit by digit, in the caller of check_if_password_long_enoguh and not in ok_pressed, and in the submit logic, the hashes are only compared. Because the check_if_password_long_enough and it’s wrappers did not have any static xrefs to any interesting function I went up the callstack again and found this function:
Again, a huge, obfuscated function I called do_program being the “main/game-loop” of our GUI up. It references the plaintext password here (and in a lot of other places) and initializes some sort of struct that it’s offset 0x58 is the plaintext password excluding the current new pressed digit. After this, the function we went over copies onto it and we can continue execution.
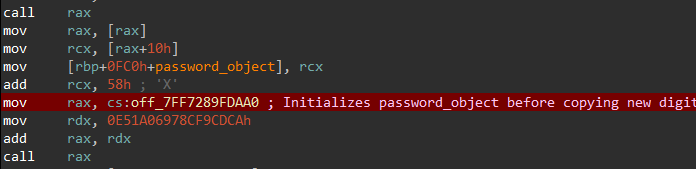
Okay, seems like we have a main password_object and a logic function do_program, let’s look at xrefs to password_object.
This xref initializes a Qt6 proprietary byte array, seems promising. The next xref calls a function with the password object and current index.
Finding Key-Press Hashing Logic
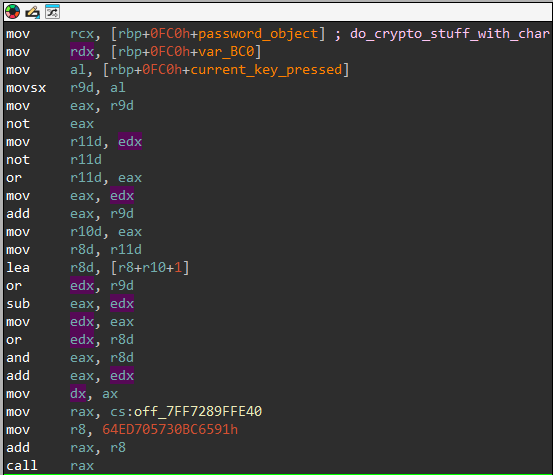
Re-enabling the hardware breakpoints we can see this function is called twice in do_program, once with rcx=password_object, dx=current_index and again with weird params, rcx still being password_object
Stepping into the call we see dx has a weird convention, it’s always the current_index*0x100 + chr(current_digit). The number is actually a 2 byte number that holds both the current index and current pressed digit, like ((char)index << 8) + chr(current_digit)
The weird thing about both of these calls is that they return some weird number, the first one returns a deterministic number, tied to the current index, and the second one a deterministic number, tied to both the current index and digit.
First call: hash_current_digit(password_object, current_index) = 0x000000000279342F Second call (I pressed 5): hash_current_digit(password_object, ((char)current_index << 8) + chr(current_digit)) = 0x000000000B740F27. The interesting thing is, when re-launching the program and pressing a different number as the first character, the first hash does not change, as expected. The second one seems to rely on both index and digit. After testing this some more I discovered there are exactly 25 options for the first hash (25 digits in the password) and 250 options for the second hash (25 indexes * 10 possible digits for each = 250).
Finding Summing of Hashes
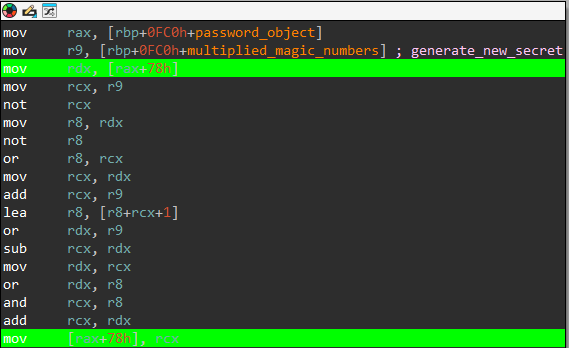
Just after the second call to hash_current_digit there is a weird imul, it’s actually between the results of the 2 calls, the first hash (index) and the second hash (index « 8 + digit).
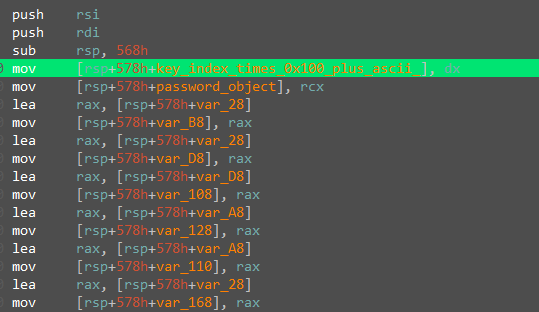
Going down one xref on this local variable we are met with the below snippet.
I know IDA’s disable breakpoint green color is horrible to look at but bear with me. The above assembly code takes in the new multiplied hashes and does some binary operations on them and saves the results in *(password_object+0x78), and also look that the previous value of this struct field comes into play. After debugging this I realized this is just a summing snippet, meaning for every digit pressed:
1
2
3
4
sum = 0
for every digit:
sum += hash(current_index)*hash(current_index << 8 + current_digit)
print(sum) -> the secret
Finding Hash Comparing Logic
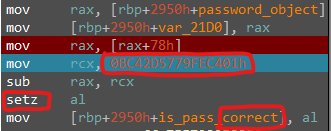
The only thing left now is to find the traces to password_object->sum_of_hash_multiplications, I’ll set a HWBP and continue execution after the last digit.
Boom! In ok_pressed as expected, there is a comparison to hardcoded number 0xBC42D5779FEC401, now lets go down one xref on is_pass_correct:
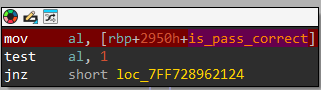
How convenient, let’s lie and jump to the other condition:
Nice! and this time we do not get the warning dialog:
Path-To-Win
Now the win condition is clear to me, I need to extract the 25+250 possible hashes and solve a summing problem of their multiplications. This looks too complicated for regular Python scripting so I’ll consider Z3.
Extracting the 2 Hash-Maps
I got 2 scripts to extract the maps of the calls to hash_current_digit, just IDA Python that sets the rdx parameter to be the index from 1 to 25 (the indexes start from 1 in this program) and after that does two loops like this:
1
2
3
4
for i in range(1, 26):
log(hash_current_digit(i))
for j in range(10):
log(hash_current_digit((i << 8) + ord(str(j))))
And a snippet from the IDA Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
FUNC_PTR = 0x00007FF7C07F1760
RCX_VAL = 0x00000079F416FC80
RIP_CALL = 0x00007FF7C0786766
for idx in range(1, ITERATIONS + 1):
rdx_val = idx
idc.set_reg_value(FUNC_PTR, "RAX")
idc.set_reg_value(rdx_val, "RDX")
idc.set_reg_value(RCX_VAL, "RCX")
idc.set_reg_value(RIP_CALL, "RIP")
idaapi.step_over()
wait_for_pause(5000)
ret = idc.get_reg_value("RAX")
print(f"[$] RAX = {hex(ret)}")
for digit in range(0, 10):
ascii_digit = ord(str(digit))
rdx_val = ((idx) << 8) + (ascii_digit)
idc.set_reg_value(FUNC_PTR, "RAX")
idc.set_reg_value(rdx_val, "RDX")
idc.set_reg_value(RCX_VAL, "RCX")
idc.set_reg_value(RIP_CALL, "RIP")
idaapi.step_over()
wait_for_pause(5000)
ret = idc.get_reg_value("RAX")
print(f"[+] RAX = {hex(ret)}")
Then saving the results into a JSON (This is the larger, 250 sized map):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
{
"1": {
"0": 174319322,
"1": 102981396,
"2": 82900395,
"3": 198250112,
"4": 263497715,
"5": 192155431,
"6": 162585309,
"7": 186059859,
"8": 54667648,
"9": 215642916
},
"..."
"25": {
"0": 7700830,
"1": 204798595,
"2": 139547600,
"3": 31632255,
"4": 96879550,
"5": 25537132,
"6": 264390352,
"7": 19441732,
"8": 156478523,
"9": 49020927
}
}
For every index, there are 10 possible hashes of the second run, and only one possible from the first one. So, when creating a data-structure of multiplications, there are exactly 10 options for each index multiplication, so when summing each one of the indexes’ multiplications we get a changing sum, that relies on a lot of different combinations.
Scripting, SAT-Solving
This is a classic problem for Z3, given I extracted all info and the summing/comparing logic this can be quite simple.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
from z3 import Solver, BitVecVal, BitVec, If, Or, And
import time
MASK64 = (1<<64)-1
second_magic = {
...
}
index_magic = [
0x0279342F,0x0C678DB8,0x087D0F40,0x0CC48D40,0x0C60A7F3,
0x0716C0D7,0x032C5F65,0x0B49D7AF,0x01B186D3,0x0545D8D5,
0x06B2F406,0x009A868C,0x07024229,0x048BDAAE,0x05F8F14F,
0x09D5D059,0x0DC0222F,0x03D1D2B6,0x0D63209A,0x0B3C02CB,
0x06FB781E,0x0F2D7EEE,0x0CA922EA,0x0ADF00DF,0x04775803
]
TARGET = 0x00BC42D5779FEC401
t0 = time.time()
digits = [BitVec(f"d{i}", 8) for i in range(25)]
s = Solver()
# Constraints on all digits
for d in digits:
s.add(d >= 0, d <= 9)
def contribution_expr(i, dvar):
index_hash = index_magic[i]
expr = None
for digit in range(10):
multiplication = (index_hash * second_magic[str(i+1)][str(digit)]) & MASK64
term = BitVecVal(multiplication, 64)
if expr is None:
expr = If(dvar == digit, term, BitVecVal(0, 64))
else:
expr = If(dvar == digit, term, expr)
return expr
# Summing hash multiplications
sum_expr = BitVecVal(0, 64)
for i in range(25):
sum_expr = sum_expr + contribution_expr(i, digits[i])
# Final check
s.add(sum_expr == BitVecVal(TARGET & MASK64, 64))
print("[+] Solving with Z3 ...")
res = s.check()
print("[+] solver check result:", res)
if res.r == 1:
m = s.model()
solution = [m[d].as_long() for d in digits]
password = ''.join(str(x) for x in solution)
print("[+] Solution:", password)
total = 0
for i,d in enumerate(solution):
total = (total + (index_magic[i] * second_magic[str(i+1)][str(d)]) ) & MASK64
print(f"[+] Computed sum -> {hex(total)}")
else:
print("[-] No solution found or solver timed out.")
1
2
3
4
5
CTF\flareon\8_-_FlareAuthenticator> python .\solve_z3.py
[+] Solving with Z3 ...
[+] solver check result: sat
[+] Solution: 4498291314891210521449296
[+] Computed sum -> 0xbc42d5779fec401
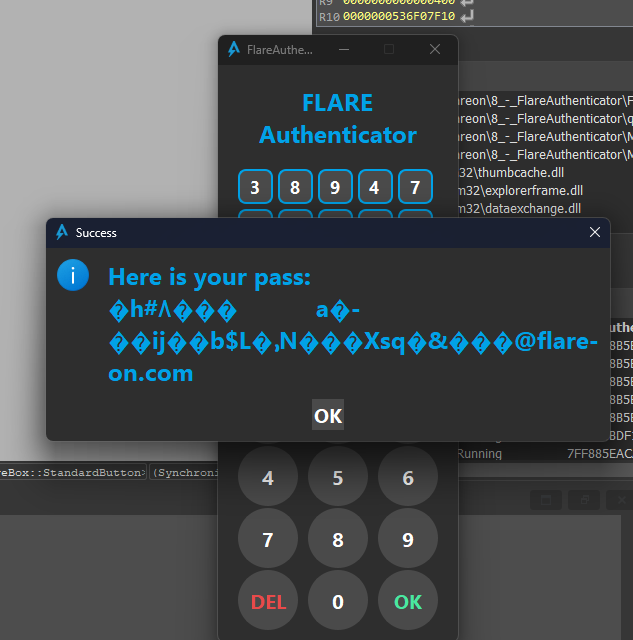
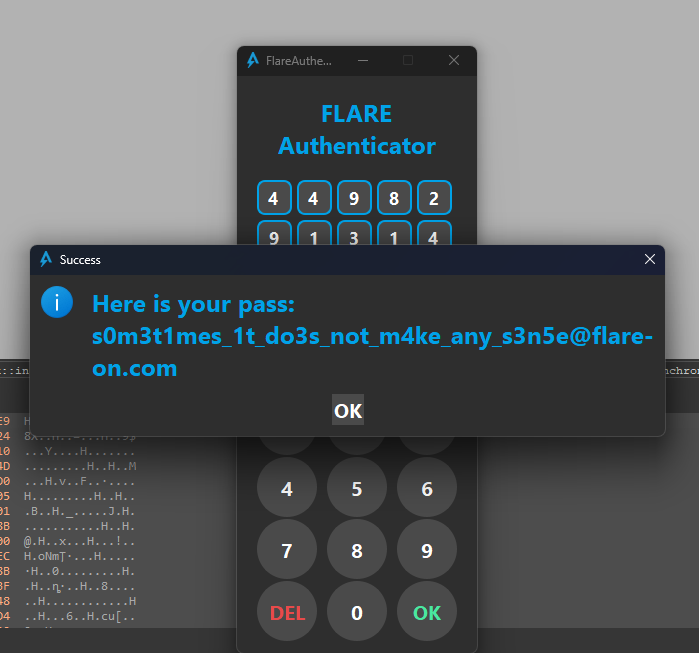
Let’s insert the password:
:)